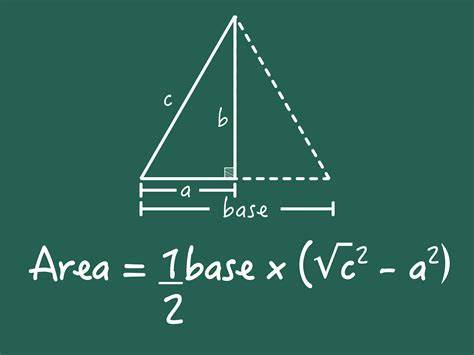ALL ABOUT TRiANGLE

 

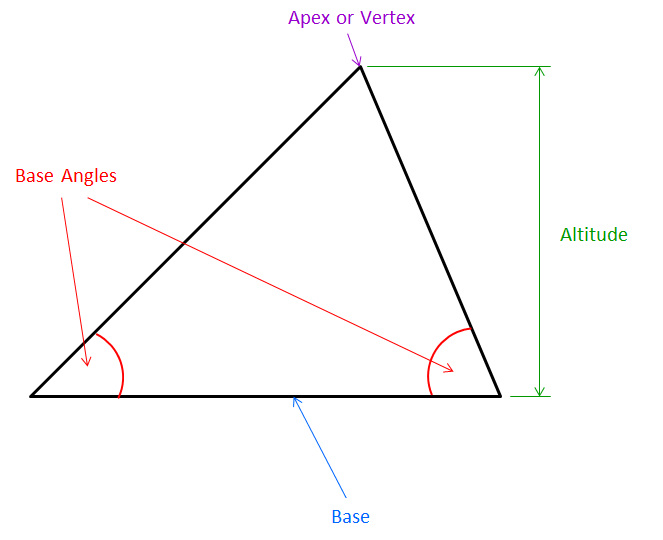
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.

In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points, when non-collinear, determine a unique triangle situated within a unique flat plane. More generally, several points in Euclidean space of arbitrary dimension determine a simplex.

In non-Euclidean geometries three straight segments also determine a triangle, for instance a spherical triangle or hyperbolic triangle. A geodesic triangle is a region of a general two-dimensional surface enclosed by three sides which are straight relative to the surface. A curvilinear triangle is a shape with three curved sides, for instance a circular triangle with circular-arc sides. This article is about straight-sided triangles in Euclidean geometry, except where otherwise noted.

A triangle with vertices   and  is denoted  In describing metrical relations within a triangle, it is common to represent the length of the edge opposite each vertex using a lower-case letter, letting  be the length of the edge   the length of  and  the length of ; and to represent the angle measure at each corner using a Greek letter, letting  be the measure of angle   the measure of  and  the measure of  

Types of triangle

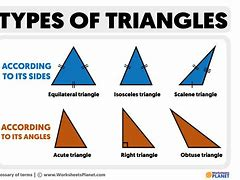
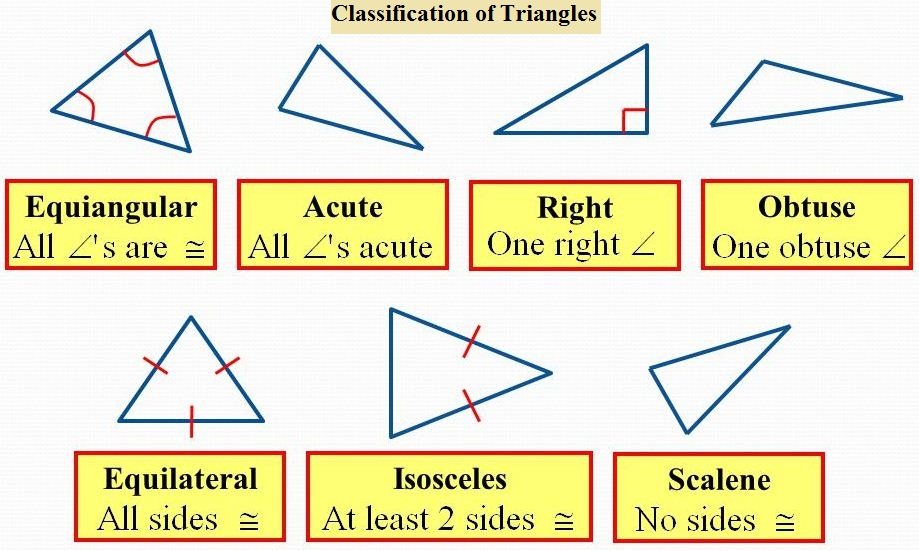
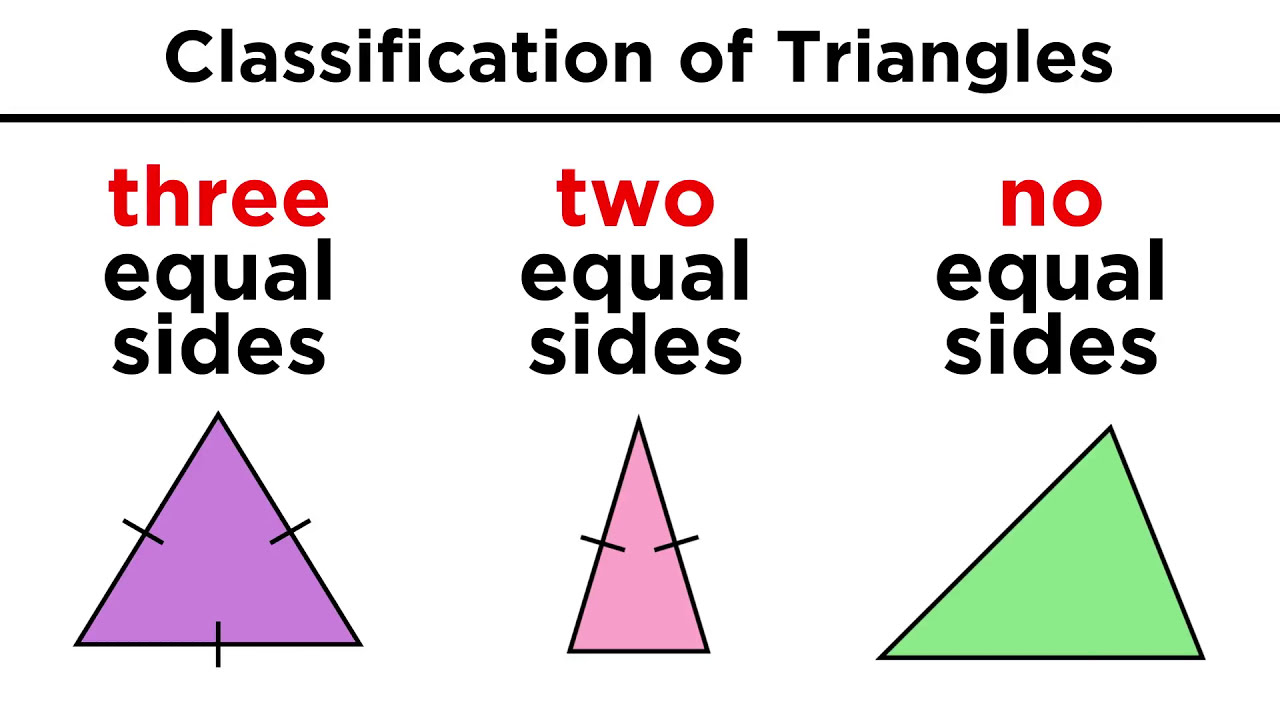The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are either a direct transliteration of Euclid's Greek or their Latin translations.

By lengths of sides :Ancient Greek mathematician Euclid defined three types of triangle according to the lengths of their sides

1.An equilateral triangle (Greek: ἰσόπλευρον, romanized: isópleuron, lit. 'equal sides') has three sides of the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°.

2.An isosceles triangle (Greek: ἰσοσκελὲς, romanized: isoskelés, lit. 'equal legs') has two sides of equal length.^{[note 1][5]} An isosceles triangle also has two angles of the same measure, namely the angles opposite to the two sides of the same length. This fact is the content of the isosceles triangle theorem, which was known by Euclid. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides.

The latter definition would make all equilateral triangles isosceles triangles. The 45–45–90 right triangle, which appears in the tetrakis square tiling, is isosceles.

3.A scalene triangle (Greek: σκαληνὸν, romanized: skalinón, lit. 'unequal') has all its sides of different lengths.^[6] Equivalently, it has all angles of different measure.

By Internal angles

Triangles can also be classified according to their internal angles, measured here in degrees.

A right triangle (or right-angled triangle) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse, the longest side of the triangle. The other two sides are called the legs or catheti^[7] (singular: cathetus) of the triangle. Right triangles obey the Pythagorean theorem: the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse: a² + b² = c², where a and b are the lengths of the legs and c is the length of the hypotenuse. Special right triangles are right triangles with additional properties that make calculations involving them easier. One of the two most famous is the 3–4–5 right triangle, where 3² + 4² = 5². The 3–4–5 triangle is also known as the Egyptian triangle.^[8] In this situation, 3, 4, and 5 are a Pythagorean triple. The other one is an isosceles triangle that has 2 angles measuring 45 degrees (45–45–90 triangle). Right triangles are fundamental in trigonometry, as they can be used to define trigonometric functions through trigonometric ratios.

Triangles that do not have an angle measuring 90° are called oblique triangles.

• A triangle with all interior angles measuring less than 90° is an acute triangle or acute-angled triangle.^[2] If c is the length of the longest side, then a² + b² > c², where a and b are the lengths of the other sides.
• A triangle with one interior angle measuring more than 90° is an obtuse triangle or obtuse-angled triangle.^[2] If c is the length of the longest side, then a² + b² < c², where a and b are the lengths of the other sides.
• A triangle with an interior angle of 180° (and collinear vertices) is degenerate. A right degenerate triangle has collinear vertices, two of which are coincident.

Basic facts:

Triangles are assumed to be two-dimensional plane figures, unless the context provides otherwise (see § Non-planar triangles, below). In rigorous treatments, a triangle is therefore called a 2-simplex (see also Polytope). Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC.

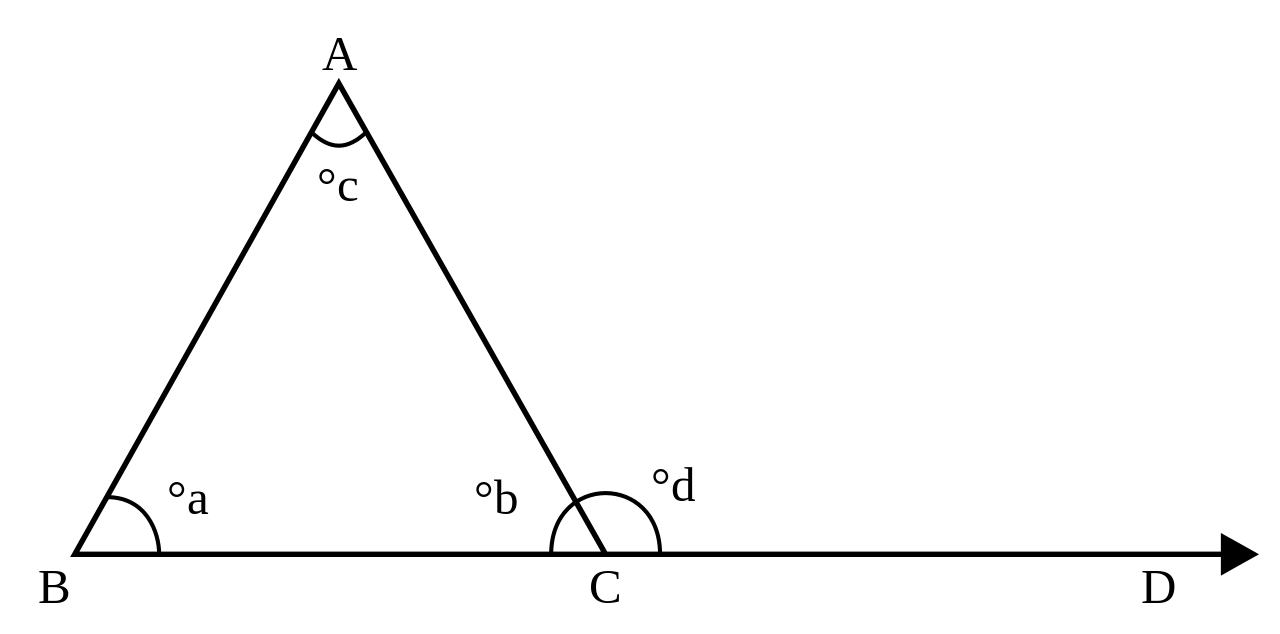
The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees.^[9][2] This fact is equivalent to Euclid's parallel postulate. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it; this is the exterior angle theorem. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees

Similarity and congruence

Two triangles are said to be similar, if every angle of one triangle has the same measure as the corresponding angle in the other triangle. The corresponding sides of similar triangles have lengths that are in the same proportion, and this property is also sufficient to establish similarity.

Some basic theorems about similar triangles are:

• If and only if one pair of internal angles of two triangles have the same measure as each other, and another pair also have the same measure as each other, the triangles are similar.
• If and only if one pair of corresponding sides of two triangles are in the same proportion as are another pair of corresponding sides, and their included angles have the same measure, then the triangles are similar. (The included angle for any two sides of a polygon is the internal angle between those two sides.)
• If and only if three pairs of corresponding sides of two triangles are all in the same proportion, then the triangles are similar.

Two triangles that are congruent have exactly the same size and shape: all pairs of corresponding interior angles are equal in measure, and all pairs of corresponding sides have the same length. (This is a total of six equalities, but three are often sufficient to prove congruence.)

Some individually necessary and sufficient conditions for a pair of triangles to be congruent are:

• SAS Postulate: Two sides in a triangle have the same length as two sides in the other triangle, and the included angles have the same measure.
• ASA: Two interior angles and the included side in a triangle have the same measure and length, respectively, as those in the other triangle. (The included side for a pair of angles is the side that is common to them.)
• SSS: Each side of a triangle has the same length as a corresponding side of the other triangle.
• AAS: Two angles and a corresponding (non-included) side in a triangle have the same measure and length, respectively, as those in the other triangle. (This is sometimes referred to as AAcorrS and then includes ASA above.)

Some individually sufficient conditions are:

• Hypotenuse-Leg (HL) Theorem: The hypotenuse and a leg in a right triangle have the same length as those in another right triangle. This is also called RHS (right-angle, hypotenuse, side).
• Hypotenuse-Angle Theorem: The hypotenuse and an acute angle in one right triangle have the same length and measure, respectively, as those in the other right triangle. This is just a particular case of the AAS theorem.

An important condition is:

• Side-Side-Angle (or Angle-Side-Side) condition: If two sides and a corresponding non-included angle of a triangle have the same length and measure, respectively, as those in another triangle, then this is not sufficient to prove congruence; but if the angle given is opposite to the longer side of the two sides, then the triangles are congruent. The Hypotenuse-Leg Theorem is a particular case of this criterion. The Side-Side-Angle condition does not by itself guarantee that the triangles are congruent because one triangle could be obtuse-angled and the other acute-angled.

Two right triangles are similar if and only if they have an acute angle of the same measure. It follows that the six possible ratios between side lengths of a right triangle depend only of the measure of one of the acute angles. These ratios are called trigonometric ratios and are commonly used as a definition of trigonometric functions.

Right triangles

The Pythagorean theorem

A central theorem is the Pythagorean theorem, which states in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. If the hypotenuse has length c, and the legs have lengths a and b, then the theorem states that

${\displaystyle {𝑎}^2+{𝑏}^2={𝑐}^2.}$

The converse is true: if the lengths of the sides of a triangle satisfy the above equation, then the triangle has a right angle opposite side c.

Some other facts about right triangles:

• The acute angles of a right triangle are complementary.

${\displaystyle 𝐴+𝐵+{90}^{\circ }={180}^{\circ }\Rightarrow 𝐴+𝐵={90}^{\circ }\Rightarrow 𝐴={90}^{\circ }-𝐵.}$

• If the legs of a right triangle have the same length, then the angles opposite those legs have the same measure. Since these angles are complementary, it follows that each measures 45 degrees. By the Pythagorean theorem, the length of the hypotenuse is the length of a leg times √2.
• In a right triangle with acute angles measuring 30 and 60 degrees, the hypotenuse is twice the length of the shorter side, and the longer side is equal to the length of the shorter side times √3:

${\displaystyle 𝑐=2𝑎}$

${\displaystyle 𝑏=𝑎\times \sqrt{3}.}$

For all triangles, angles and sides are related by the law of cosines and law of sines (also called the cosine rule and sine rule).

Area of a triangle 

It is the region enclosed by it, in a two-dimensional plane. As we know, a triangle is a closed shape that has three sides and three vertices. Thus, the area of a triangle is the total space occupied within the three sides of a triangle. The general formula to find the area of the triangle is given by half of the product of its base and height.

In general, the term “area” is defined as the region occupied inside the boundary of a flat object or figure. The measurement is done in square units with the standard unit being square meters (m2). For the computation of area, there are predefined formulas for squares, rectangles, circles, triangles, etc. In this article, we will learn the area of triangle formulas for different types of triangles, along with some example problems.

The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e. A = 1/2 × b × h. Hence, to find the area of a tri-sided polygon, we have to know the base (b) and height (h) of it. It is applicable to all types of triangles, whether it is scalene, isosceles or equilateral. To be noted, the base and height of the triangle are perpendicular to each other. The unit of area is measured in square units (m2, cm2).

Area of a Right Angled Triangle

A right-angled triangle, also called a right triangle has any one angle equal to 90°. Therefore, the height of the triangle will be the length of the perpendicular side.

Area of an Equilateral Triangle

An equilateral triangle is a triangle where all the sides are equal. The perpendicular drawn from the vertex of the triangle to the base divides the base into two equal parts. To calculate the area of the equilateral triangle, we have to know the measurement of its sides.

• Area of an Equilateral Triangle = A = (√3)/4 × side2

Area of an Isosceles Triangle

An isosceles triangle has two of its sides equal and also the angles opposite the equal sides are equal.

Area of Triangle with Three Sides (Heron’s Formula)

The area of a triangle with 3 sides of different measures can be calculated using Heron’s formula. Heron’s formula includes two important steps. The first step is to find the semi perimeter of a triangle by adding all three sides of a triangle and dividing it by 2. The next step is to apply the semi-perimeter of triangle value in the main formula called “Heron’s Formula” to find the area of a triangle.

where, s is semi-perimeter of the triangle = s = (a+b+c) / 2 

Example 1:

Find the area of an acute triangle with a base of 13 inches and a height of 5 inches.

Solution:

A = (½)× b × h sq.units

⇒ A = (½) × (13 in) × (5 in)

⇒ A = (½) × (65 in2)

⇒ A = 32.5 in2

Example 2:

Find the area of a right-angled triangle with a base of 7 cm and a height of 8 cm.

Solution:

A = (½) × b × h sq.units

⇒ A = (½) × (7 cm) × (8 cm)

⇒ A = (½) × (56 cm2)

⇒ A = 28 cm2

Example 3:

Find the area of an obtuse-angled triangle with a base of 4 cm and a height 7 cm.

Solution:

A = (½) × b × h sq.units

⇒ A = (½) × (4 cm) × (7 cm)

⇒ A = (½) × (28 cm2)

⇒ A = 14 cm2

-----------------------------------------------------------------------------------------------------------------------------

By 

MRUDULA GURADE F.Y.B.Ed

MAMATA KUSHWAHA F.Y.B.Ed